Lecture #4: Causal ordering of message and global state

These topics are from Chapter 5.5-5.10 in Advanced Concepts in OS.

Topics for today

• Review
• The Birman-Schiper-Stephenson protocol for causal ordering of messages
• Chandy-Lamport global state recording algorithm
• Huang's termination algorithm

Review

• How is the happened before relation defined?
• How do we maintain Lamport's logical clock (rules?)?
• How do we maintain vector clocks? What do they offer?
• What is the causal ordering of messages?

Birman-Schiper-Stephenson Protocol for the causal ordering of messages.

Global State Problem

How to collect or record a coherent (consistent) snapshot of the state of an entire distributed system?

One application of this problem is in implementing a breakpoint for debugging a distributed application. That is, suppose we want to suspend execution of all the processes in a way that we can examine what each of them is doing, and later resume them.

Banking Example

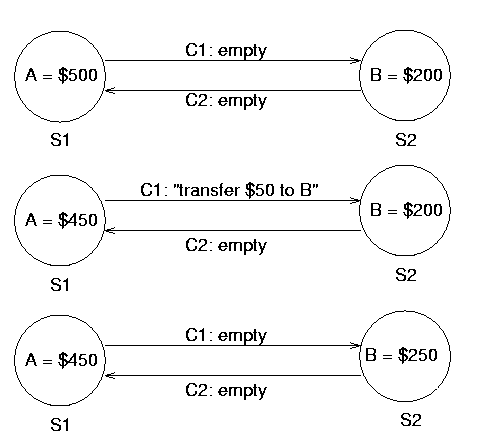
For consistency, we need to take into account the messages that are in transit.

Let n be the number of messages sent by A along a channel before A's state is recorded, n' be the number of messages sent by A along the channel before the channel's state is recorded, a consistent global state requires n = n'

In the global state we want to view as in-transit all the messages sent along a channel before the sender's state was recorded that were not yet received when the receivers state was recorded.

A global state includes snapshots of the states of all the channels along with the states of all the sites. Since the channels are passive, the snapshots of the channels must be computed by the sites to which they are connected.

Global State: Notation

For a site S_i, its local state, LS_i, at a given time is defined by the local context of the application.

send(m_i,j) is the event of S_i sending message m_i,j to S_j

rec(m_i,j) is the event of S_j receiving message m_i,j from S_i

time(x) is the time at which state x was recorded

time(send(m)) is the time at which message m was sent

send(m_i,j) Î LS_i iff time(send(m_i,j)) < time(LS_i)

rec(m_i,j) Î LS_i iff time(rec(m_i,j)) < time(LS_j)

GS = { LS₁, LS₂, ¼LS_n}

Global State: Definitions

transit(LS_i, LS_j) = {m_i,j | send(m_i,j) Î LS_i and rec(m_i,j) Ï LS_j}

inconsistent(LS_i, LS_j) = {m_i,j | send(m_i,j) Ï LS_i and rec(m_i,j) Î LS_j}

GS is consistent iff it is not inconsistent.
GS is strongly consistent if it consistent and transitless.

In a consistent global state, causes are recorded if the corresponding effects are recorded.

In a strongly consistent global state, causes are recorded iff the corresonding effects are recorded.

Example

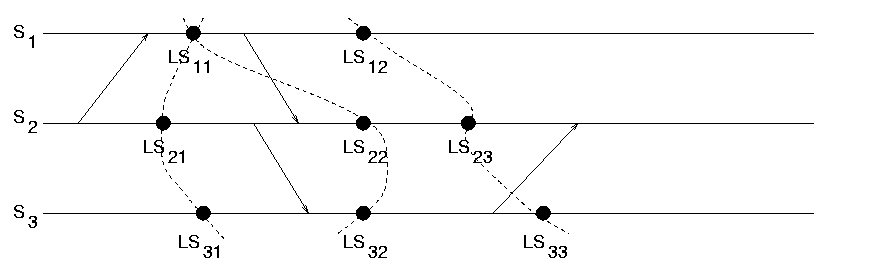
{LS₁₂, LS₂₃, LS₃₃} is consistent.

{LS₁₁, LS₂₂, LS₃₂} is inconsistent.

{LS₁₁, LS₂₁, LS₃₁} is strongly consistent.

Chandy-Lamport GS Recording Algorithm

Uses a marker message to initiate taking the snapshot, and to separate messages within each channel.

Chandy-Lamport GS Recording Alg: Sending Rule

• P records its local state
• For each outgoing channel C from P on which a marker has not already been sent, P sends a marker along C before P sends further messages along C

Chandy-Lamport Receiving Rule

• if Q has not recorded its state then
  • record the state of C as an empty sequence
  • follow the Marker Sending Rule
• else
  • record the state of C as the sequence of messages received along C after Q's state was recorded and before Q received the marker along C

Chandy-Lamport Example

Suppose site S₀ sends markers to sites $ S₁and S_2$, and site S₂, with account B, receives the marker first, checkpointing the valuer of B in a local snapshot. The request message "[B+=$50]" arrives later, before the marker on channel C1, and so is recorded as part of the state of that channel.

How does this algorithm get the data back to the process that requested the snapshot? How does the algorithm terminate?

Usefulness of Recorded Global State

• limited to detecting stable properties of a system
  Why?
• examples of stable properties:
  • deadlock
  • termination of a computation

Termination Detection

• Needed in many distributed algorithms: deadlock detection, deadlock resolution.
• An example of using the consistent global view.

System model:

• every process is either active or idle
• only active processes send messages
• an active process may become idle at any time
• an idle process can only become active by receiving a computation message
• a computation has terminated iff
  • all process are idle
  • there are no messages in transit

Huang's Termination Algorithm

• one process is the controlling agent
• computation involves exchanges of messages
• each process has a weight between 0 and 1
• when a process sends a message, it splits its weight between itself and the message
• B(DW) = computation messages with weight DW
• C(DW) = control message with weight DW
• invariant: the sum of all process weights is 1
• initially all processes are idle,
  controlling agent has weight 1, and others have weight 0
• sending a message splits weight
  between sender and receiver
• computation starts when controlling agent sends a message
• computation terminates when controlling agent weight = 1 again

This algorithm views termination as a flow analysis problem.

Details

• process with weight W sends computation message to P
  • split W = W₁ + W₂
  • set W to W₁ and send B(W₂) to P
• process P with weight W receives B(DW)
  • set W to W + DW
  • if P was idle, P becomes active
• when a process becomes idle
  • send C(W) to the controlling agent
  • set W to 0
• when the controlling agent receives C(DW)
  • set W to W + DW
  • if W = 1 the computation has terminated

Proof of correctness

Things for you to do

• Review Chapter 5 and understand the Schiper-Eggli-Sandoz protocol. A quiz will be given in the next class.