Efficient FFT Implementations

A simple optimization, can rewrite the final loop reusing t = wy_k^[1], this is a butterfly operation.

for k ¬ 0 to n/2 - 1

   do t ¬ wy_k^[1],

        y_k ¬ y_k^[0] + t

        y_k + n/2 ¬ y_k^[0] - t

        w ¬ w w_n

Let's analyze the data used in Recursive-FFT. The figure shows where coefficients are moved on the way down, with an initial vector of length 8.

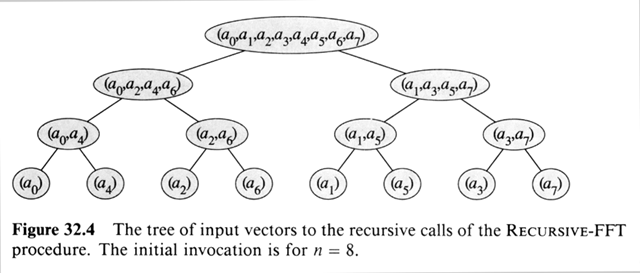
All evens move right, the odds to the left. Each Recursive-FFT make two more calls, until we hit vectors of length 1. If instead of the order ( a₀, a₁, a₂, a₃, a₄, a₅, a₆, a₇ ) we could use ( a₀, a₄, a₂, a₆, a₁, a₅, a₃, a₇ ) then we could traverse the tree with data in place. This algorithm would start at the bottom and work up using DFT's to take 2 1's to a 2,  2 2's to a 4, etc. Consider the array A [ 0...n-1 ] as originally holding a in the order of the leaves. We then iterate on the levels s, as follows:

FFT-Base ( a )

1.  n ¬ length[a]

2. for s ¬ 1 to lg n

3.    do m ¬ 2^s

4.     w_m ¬ e^{( 2 p i / m )}

5.     for k ¬ to n - 1 by m

6.     do w ¬ 1

7.        for j ¬ 0 to m/2 - 1

8.           do t ¬ wA[k + j + m/2]

9.                u ¬ A[k + j]

10.                A[k + j] ¬ u + t

11.                A[k + j + m/2] ¬ u - t

12.                w ¬ ww_n

This code "butterflies" up from the bottom level. It also identifies:

A[k ...k + 2^s-1 - 1] with y ^[0]  and A[k+ 2^s-1 ...k + 2^s - 1] with y ^[1]

By adding the code to put a into A[] in the right order the code is complete.

Iterative-FFT ( a )

1. Bit-Reverse-Copy ( a, A )

2. n length[a]

3. for s ¬ 1 to lg n

4.    do m ¬ 2^s

5.       w_m ¬ e^{( 2 p i / m )}

6.       w ¬ 1

7.          for j ¬ 0 to m/2 - 1

8.             do for k j to n - 1 by m

9.                do t ¬ wA[k +m/2]

10.                     u ¬ A[k]

11.                     A[k] ¬ u + t

12.                     A[k + m/2] ¬ u - t

13.              w ¬ ww_n

14. return A

The trick is Bit-Reverse-Copy ( a, A ) The desired order (with n = 8) is 0, 4, 2, 6, 1, 5, 3, 7 or in binary 000, 100, 010, 110, 001, 101, 011, 111 if we "bit reverse" 000, 001, 010, 011, 100, 101, 110, 111 we get the integers in order. This is what we need to do.

Parallel FFT Circuit

Using the idea of the iterative FT we can map this into a parallel algorithm where each "level" is one of the lg n outer loops as follows:

Note: there are lg n levels each doing  Q ( n ) work. so in parallel this algorithm takes  Q (n lg n) time.