Breadth-First Search

Breadth-first search: a method to search a graph and an exemplar of many important graph algorithms. Given G = ( V, E ), chose a vertex, s, to be the source. Move out from s, systematically to find all v Î V that are accessible from s, and compute their distances from s. Distance from s to v is the "shortest path".

Words: start at s, find all vertices distance 1 from s, keep going until all vertices have been discovered.

Dye analogy: s is the dye injection point and you watch the progress of the dye through the graph. Each time step a single edge is crossed. In breadth-first search, each vertex is colored:

1. White: not yet discovered

2. Gray: discovered but still some undiscovered adjacent vertices .

3. Black: discovered and all adjacent vertices discovered

Gray vertices are the frontier/interface between discovered/undiscovered.

Constructing a breadth-first tree:

1. Start with s (the root)

2. Scan the adjacency list of all previously discovered nodes. If u was previously discovered and we just found v, then we add v. u is the predecessor/parent of v in the breadth-first tree.

This progresses, iteratively. Note: Start with all nodes white. When you first encounter a white node, you make it gray. When you go through that node's adjacency list, you make it black.

Code: Store

1. Color (white or gray or black)

2. Predecessor p[n]

3. Distance from s d[n]

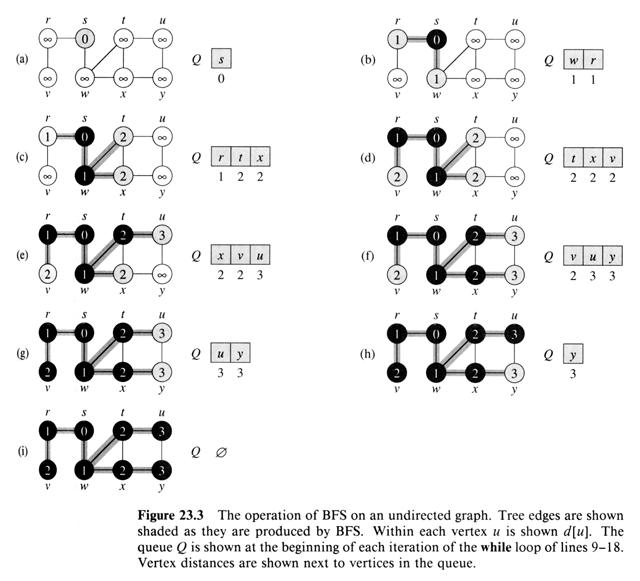
BFS ( G, s )

1. for each vertex u Î V[G] - {s}

2.    do color [u] ¬ white  // white out all but s

3.      d[u] ¬ ¥

4.      p[u] ¬ nil

5. color [s] ¬ gray // s starts out gray

6. d[s] ¬ 0

7. p[s] ¬ nil

8. Q ¬ {s} // end initialization

9. while Q ¹ Æ

10.    do u ¬ head[Q]

11.       for each v Adj[u]

12.          do if color[v] = white

13.               then color[v] ¬ gray

14.                  d[v] ¬ d[u] + 1

15.                    p[v] ¬ u

16.                   Enqueue ( Q, v )

17.        Dequeue ( Q ) // Q stores grays

18.        color[u] ¬ black // all of u's adjacents have been seen, so color it black and                              //  move on

Running time of Breadth-First search:

1. Each node is enqueued once (white ® gray)

2. Each node is dequeued once (gray ® black)

3. Each adjacency list is scanned only once.

1. O ( | V | )

2. O ( | V | )

3. O ( | E | )

Overall running time is O ( | V | + | E | ). Clearly better to use the adjacency list representation. (What differs with the matrix representation?)

Shortest-path distance: d ( s, v ) is the minimum number of  edges in any path from s to v, or ¥ if there is no path. A path from s to v with distance d ( s, v ) is a shortest-path. Note, there may be more than one shortest path.

Lemma: Let G = ( V, E ) be a graph, s Î V an arbitrary vertex, then " ( u, v ) Î E d ( s, v ) £ d ( s, v ) + 1. If u is reachable from s, then it holds. If not then both d ( s, v ) = ¥ and it holds.

Suppose BFS is run on G from s. " v Î V d[v] ³ d ( s, v )

 Induction on vertices:

1. d[s] = 0 = d ( s, s )

2. d[v] =  ¥ ³ d ( s, v ) " s ¹ v at the first step

v is discovered from u (u is at the head of Q), v is white.

Induction when u is at the head of Q

Assume d[u] ³ d ( s, v )

d[v] = d[u] + 1

       ³ d ( s, v )  + 1

       ³ d ( s, v )

Proved.

Suppose during BFS Q contains v₁, ... v_v) Þ d[v_v] £ d[v₁],  d[v_i] £ d[v_i+1], i = 1, ..., v - 1

Proof:

Induction on queue operations.

1. When Q = <s> it holds

2. Must prove it holds after both dequeuing and enqueuing a vertex when v₁ is is dequeued v₂ becomes the head

d[v_r] £ d[v₁] + 1 £ d[v₂] + 1            Ö

What happens we enqueue? v_v+1 is enqueued Adj[v₁] v_v+1.

d[v_v+1] = d[v₁] + 1          Ö

d[v_v] £ d[v₁] + 1 = d[v_v+1]           Ö

Let G = ( V, E ) and s Π V for BFS.

1. BFS discovers all v Π V that are reachable from s

2. d[v] = d ( s, v ) " v Π V (even ¥)

3. " v ¹ s reachable, a shortest path is the shortest path from s to p[v] followed on ( p[v], v )

Proof:

If v is unreachable it's true. d[v] = ¥ = d ( s, v ). If v is reachable from s define:

V_k = { v Î V: d ( s, v ) = k}

Inductions on k, " v Î V_k

• v is grayed

• d[v] = k

• if v ¹ s, p[v] = u Î V_k-1

• v is enqueued in Q

the above 4 bullets all happen during the same loop

k = 0 = V₀ {s}           Ö

Q is never empty until the end. Once u is enqueued, d[u] and p[u] are set and do not change. From previous results we have that d[v_i] £ d[v_i+1], and v Î V_k Þ d[v] ³ k and v is discovered after all V_k-1 vertices are enqueued. Since d ( s, v ) = k $ u Î V_k-1 '( u, v ) Î E. Let u be the first of these grayed. U  must also eventually appear at the head of Q, when it is Adj[u] is scanned and v is discovered, this is the first time it could be (would be in V_k-1, then).

BFS:

d[v] = d[u] + 1

p[v] = u

enqueues           Ö

 This proof by induction is done.  (Clearly ( p[u], u )is in a shortest path.)

Breadth-First Trees:

G = ( V, E ), s Î V source. G = ( V_p, E_p ) is the predecessor sub graph. V_p = { v Î V | p[v] ¹ nil } v {s} (accessible vertices) E_p = { ( p[v], v )  Î E :  v Î V_p - {s}} (tree edges) . G_p  is a breadth first tree. " v Π V_p $ a unique simple path from s to v.

BFS to G constructs p so G_p is a BF Tree.

Proof:

v Î V_p  only if reachable p[v] = u only if ( v, v ) E by previous the unique path must be the shortest.

Print-Path ( G, s, v )

1. if v = s

2.    then print s

3.    else if p[v] = nil

4.       then print "no path from " s "  to " v " exists"

5.       else Print-Path ( G, s, p[v] )

6.          print v

Prints out the vertices from s to b in G.