Elements of Dynamic Programming

We have done an example of dynamic programming: the matrix chain multiply problem, but what can be said, in general, to guide us to choosing DP?

  • Optimal Substructure

  • Overlapping Sub-problems

  • Variant: Memoization

Optimal Substructure: OS holds if optimal solution contains within it optimal solutions to sub problems. In matrix-chain multiplication optimally doing A1, A2, A3, ...,An required A 1...k and  A k+1 ...n to be optimal. It is often easy to show the optimal sub problem property as follows:

  1. Split problem into sub-problems

  2. Sub-problems must be optimal, otherwise the optimal splitting would not have been optimal.

There is usually a suitable "space" of sub-problems. Some spaces are more "natural" than others.

For matrix-chain multiply we chose sub-problems as sub chains. We could have chosen all arbitrary products, but that would have been much larger than necessary! DP based on that would have to solve too many sub-problems.

A general way to investigate optimal substructure of a problem in DP is to look at optimal sub-, sub-sub, etc. problems for structure. When we noticed that sub problems of A1, A2, A3, ...,An consisted of sub-chains, it made sense to use sub-chains of the form Ai, ..., Aj as the "natural" space for sub-problems.

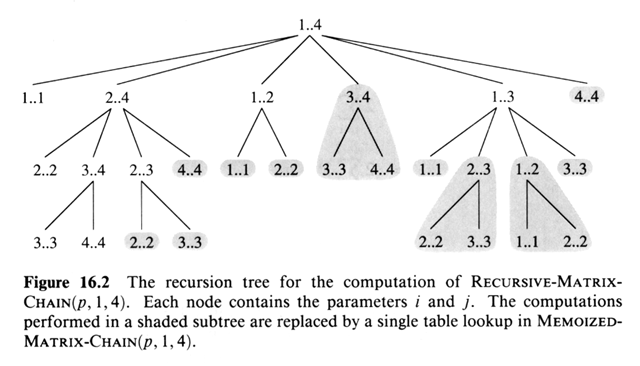
Overlapping Sub-problems: Space of sub-problems must be small: recursive solution re-solves the same sub-problem many times. Usually there are polynomially many sub-problems, and we revisit the same ones over and over again: overlapping sub-problems.

Recursive-Matrix-Chain (p, i, j) (inefficient recursive program)

  1. if i = j

  2.    then return 0

  3. m[i,j] ¬ ¥

  4. for k ¬ i to j - 1

  5.    do q ¬ Recursive-Matrix-Chain (p, i, k )  + Recursive-Matrix-Chain (p, k + 1, j) + pi-1 pk pj

  6.          if q < m[i,j]

  7.             thenm[i,j] ¬ q

  8. return m[i,j]

With divide-and-conquer, each sub-problem is new, in DP, most of the sub-problems are old. Thus storing solutions to sub-problems with DP in a lookup table saves loads of time.

T (n) = running time to compute m[1,n] by the above recursive algorithm:

i = j and q < m[i,j] unit time are running time assumptions

T (1) ³ 1

T (n) ³  1 +
n - 1
å
k = 1 		 ( T (k) + T ( n - k ) + 1 )
        ³     2
n - 1
å
i = 1 		  T (i) +  n

Will show T (n) ³ 2n-1 ( = W (2n))

Induction n = 1, T (1) ³ 21-1 = 1 Ö

Assume true for up to n:

    T (n)    ³     2
n - 1
å
i = 1 		  2i-1 +  n

= 2 ( 1 + 21 + 22 + ... + 2n-2 ) + n

= 2 ( (2n-1 -1) / ( 2 - 1 )) + n

= 2 ( 2n-1 - 1 ) + n

= 2n - 2 + n ³ 2n-1 ( true when n ³ 2 !!)

Recall: DP Q ( n2) sub-problems solved. Rule of thumb: Whenever a recursive approach solves the same problem repeatedly this signals a good DP candidate.

Memoization: What if we stored sub-problems and used the stored solutions in a recursive algorithm? This is like divide-and-conquer, top down, but should benefit like DP which is bottom-up. Memoized version maintains an entry in a table. One can use a fixed table or a hash table.

Memoized-Matrix-Chain (p)

  1. n ¬ length[p] - 1
  2. for i ¬ 1 to n
  3.    do for j ¬ i to n
  4.       do m[i,j] ¬ ¥ (initialize to "undefined" table entries)
  5. return Lookup-Chain (p, 1, n)

Lookup-Chain (p, i, j)

  1. if m[i,j] <   ¥ (see if we know or not)
  2.    then return m[i,j]
  3. if i = j
  4.    then m[i,j] ¬ 0
  5.    else for k ¬ i to j - 1
  6.       do q ¬ Lookup-Chain (p, i, k) + Lookup-Chain (p, k + 1, j) + pi-1 pk pj
  7.             if q < m[i,j]
  8.                then m[i,j] ¬ q
  9. return m[i,j]


Each call is either:

O (1) if m[i,j] was previously computed

O (n) if not

Each m[i,j] called many times, but initialized only once. O ( n n2 ) Memoization turns W (2n) ® O ( n3 )!
Dynamic Programming - 2 of 3