Derivations and parse trees
Regular expressions are formed by the use of three mechanisms
Tokens are the basic lexical unit for a programming language
$$number \rightarrow integer | real $$ $$integer \rightarrow digit\ digit* $$ $$real \rightarrow\ integer\ exponent\ |\ decimal\ (\ exponent\ |\ \epsilon\ )$$ $$decimal \rightarrow\ digit*\ (\ .\ digit\ |\ digit\ .\ )\ digit*$$ $$exponent \rightarrow\ (\ e\ |\ E\ )\ (\ +\ |\ -\ |\ \epsilon\ )\ integer$$ $$digit \rightarrow\ 1\ |\ 2\ |\ 3\ |\ 4\ |\ 5\ |\ 6\ |\ 7\ |\ 8\ |\ 9\ |\ 0$$
You can consider the previous set of rules as a generator for the initial token "number"; starting with the first rule, you can expand each.
For instance,
$$number \Rightarrow integer \Rightarrow digit\ digit*$$ $$\ \Rightarrow 1\ digit* \Rightarrow 1\ 3\ digit* \Rightarrow 1\ 3$$
Some languages ignore case (most Basics, for instance); many impose rules about the case of keywords / reserved words / built-ins; others use case to imply semantic content (Prolog and Go, for instance)
Some languages support more than just ASCII
Most languages are free format, with whitespace only providing separation, not semantics
However, line breaks are given some significance in some languages, such as Python and Haskell
"a4b6" =~ /a([0-9])b([0-9])/$ perl
"a4b6" =~ /a([0-9])b([0-9])/ ;
print $1 . "\n";
print $2 . "\n";
4
6While regular expressions are ideal for identifying individual tokens, adding recursion to the mix means that we can now recognize "context-free grammars". Context-free grammars have the advantage of allowing us to specify more flexible structure than mere regular expressions.
Each rule is called a production. The symbols that appear on the left-hand side of a production rule are called non-terminals.
$$op \rightarrow +\ |\ -\ |\ *\ |\ /$$
$$op \rightarrow +$$ $$op \rightarrow -$$ $$op \rightarrow *$$ $$op \rightarrow /$$
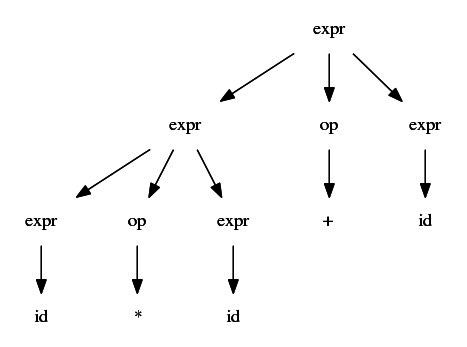
$$expr \rightarrow id\ |\ number\ |\ -\ |\ expr\ op\ expr\ |\ (\ expr\ )$$ $$op \rightarrow +\ |\ -\ |\ *\ |\ /$$
$$expr \Rightarrow expr\ op\ expr\ \Rightarrow expr\ op\ id \Rightarrow expr\ +\ id$$ $$\Rightarrow expr\ op\ expr\ +\ id\ \Rightarrow expr\ op\ id\ +\ id\ \Rightarrow expr\ *\ id\ +\ id$$ $$\Rightarrow id\ *\ id\ +\ id$$
$$expr \Rightarrow^{\star} id\ *\ id\ +\ id$$

$$expr \rightarrow term\ |\ expr\ addop\ term$$ $$term \rightarrow factor\ |\ term\ multop\ factor$$ $$factor \rightarrow id\ |\ number\ |\ -\ factor\ |\ (\ expr\ )$$ $$addop \rightarrow\ +\ |\ -$$ $$multop \rightarrow\ *\ |\ /$$
Usually, scanning is the fast, easy part of syntax analysis; it is usually linear or very close to it; importantly, it removes the detritus of comments and preserves semantically significant strings such as identifiers. (Note the weasel word "usually"!)
Examples of scanner generators are lex, flex, re2c, and Ragel.
$$(S,\Sigma,Move(),S0,Final)$$
where S is the set of all states in the NFA, Sigma is the set of input symbols, Move is the transition() function that maps a state/symbol pair to sets of states, S0 is the initial state, and Final is the set of accepting/final states. (See section 3.6 of the Dragon Book).
An NFA is entirely general since it allows both:
A deterministic finite automaton is a type of NFA where
Both an NFA and a DFA are equivalent in expressive power, and can always be transformed from one to the other.
A parser is a language recognizer. We generally break parsers up into two CFG families, LL and LR.
Parsing has generally the arena for context-free grammars, but other techniques have recently gained quite a bit of attention. Packrat parsing, PEGs, and parser combinators have recently become areas of interest since these methodologies seems to offer some benefits over traditional techniques. Surprisingly, the 4th edition does not cover any ground on this current topic.
LL parsers are top-down parsers, and usually written by hand (good old recursive-descent parsing!)
LR parsers are bottom-up parsers, and are usually created with a parser generator. (Also see SLR parsing, as referenced in your book on page 70.)
LL stands for "Left-to-right, Left-most derivation"
LR stands for "Left-to-right, Right-most derivation"
$$idlist \rightarrow id\ idlisttail$$ $$idlisttail \rightarrow ,\ id\ idlisttail$$ $$idlisttail \rightarrow ;$$
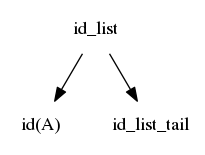
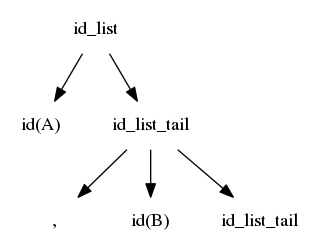
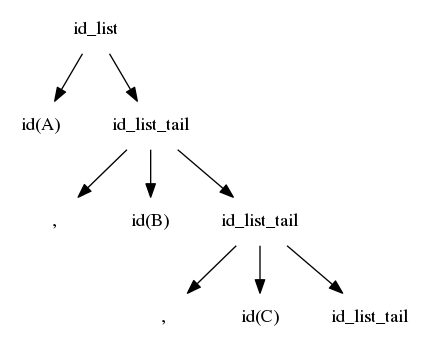
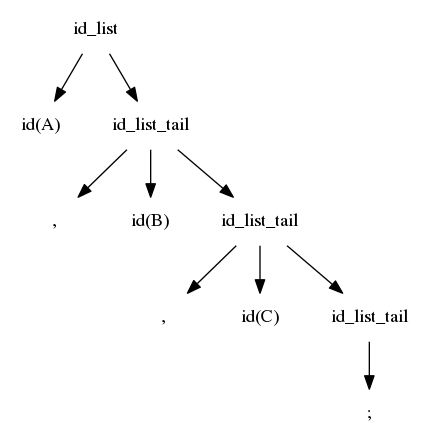
We reverse the search; we again start at the left, but we are now trying to match from the right
The first match is when id_list_tail matches ";"
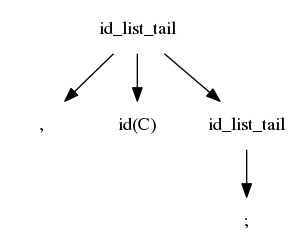
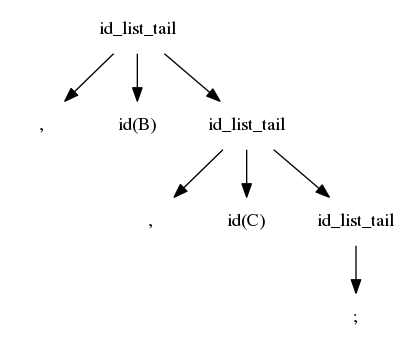
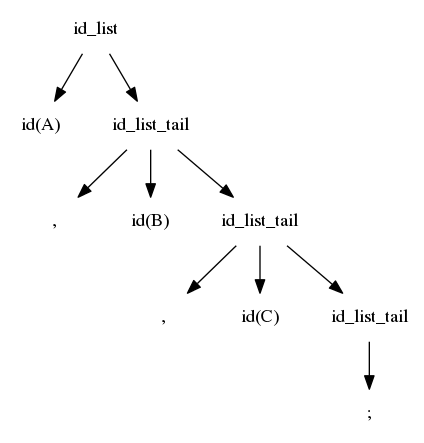
$$idlist \rightarrow idlistprefix\ ;$$ $$idlistprefix \rightarrow idlistprefix\ ,\ id$$ $$idlistprefix \rightarrow id$$
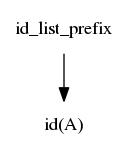
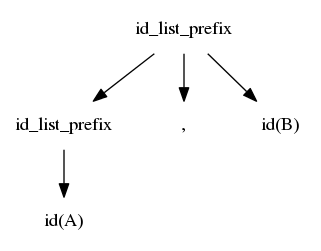
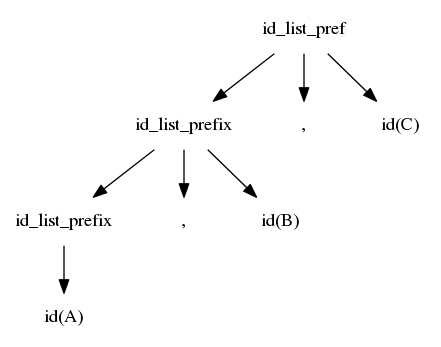
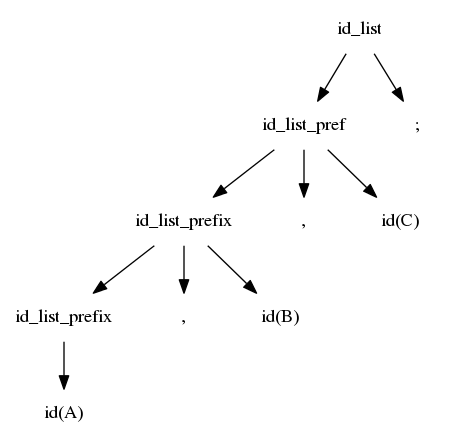
As your book mentions on page 72, GCC is now using a hand-written recursive descent parser rather than bison.
This is also true for clang.
$$program \rightarrow stmtlist\ EOD$$ $$stmtlist \rightarrow stmt\ stmtlist\ |\ \epsilon$$ $$stmt \rightarrow id\ :=\ expr\ |\ read\ id\ |\ write\ expr$$ $$expr \rightarrow term\ termtail$$ $$termtail \rightarrow addop\ term\ termtail\ |\ \epsilon$$
$$term \rightarrow factor\ factortail$$ $$factortail \rightarrow multop\ factor\ factortail\ |\ \epsilon$$ $$factor \rightarrow (\ expr\ )\ |\ id\ |\ number$$ $$addop \rightarrow +\ |\ -$$ $$multop \rightarrow *\ |\ /$$
read A
read B
sum := A + B
write sum
write sum / 2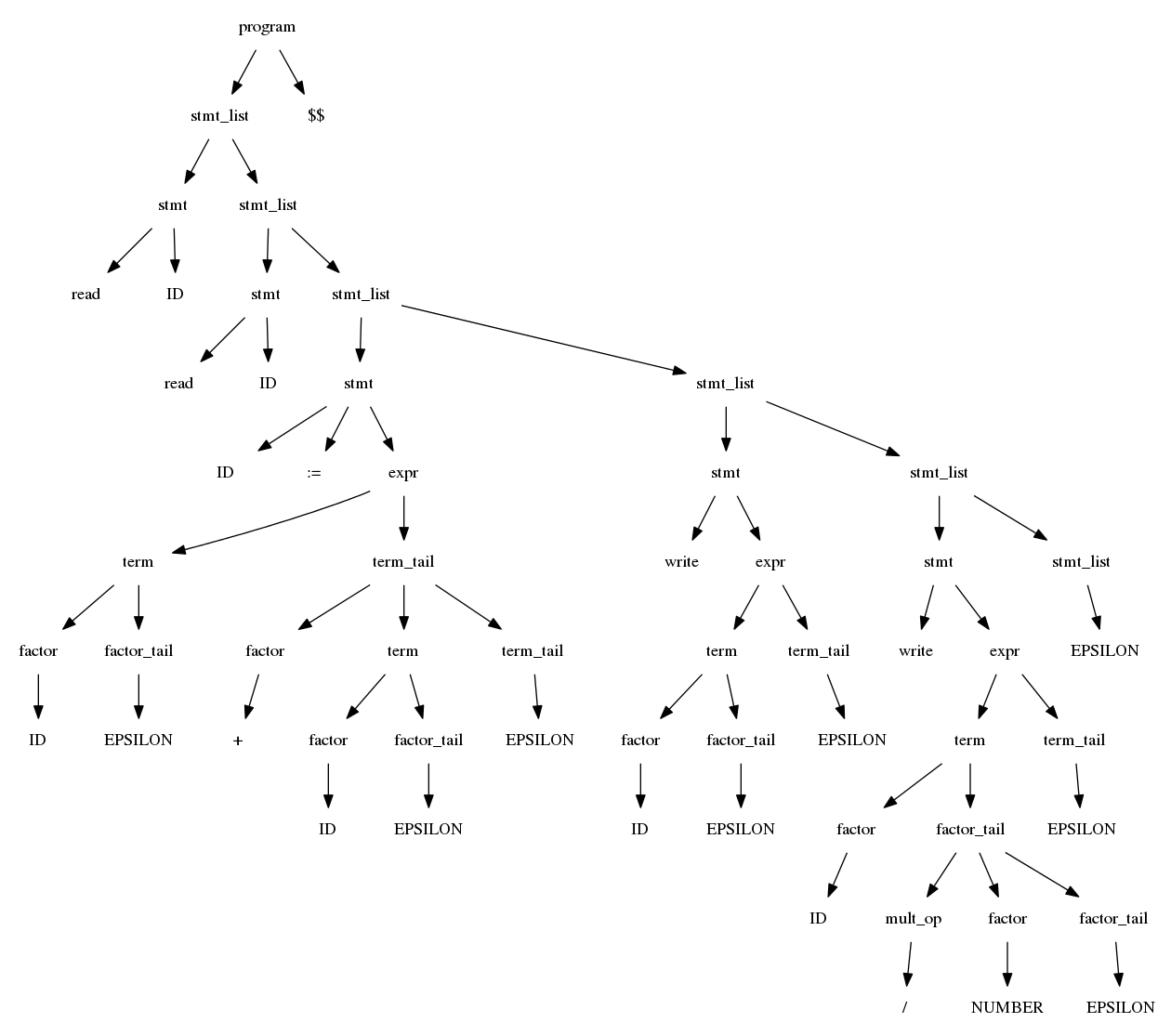
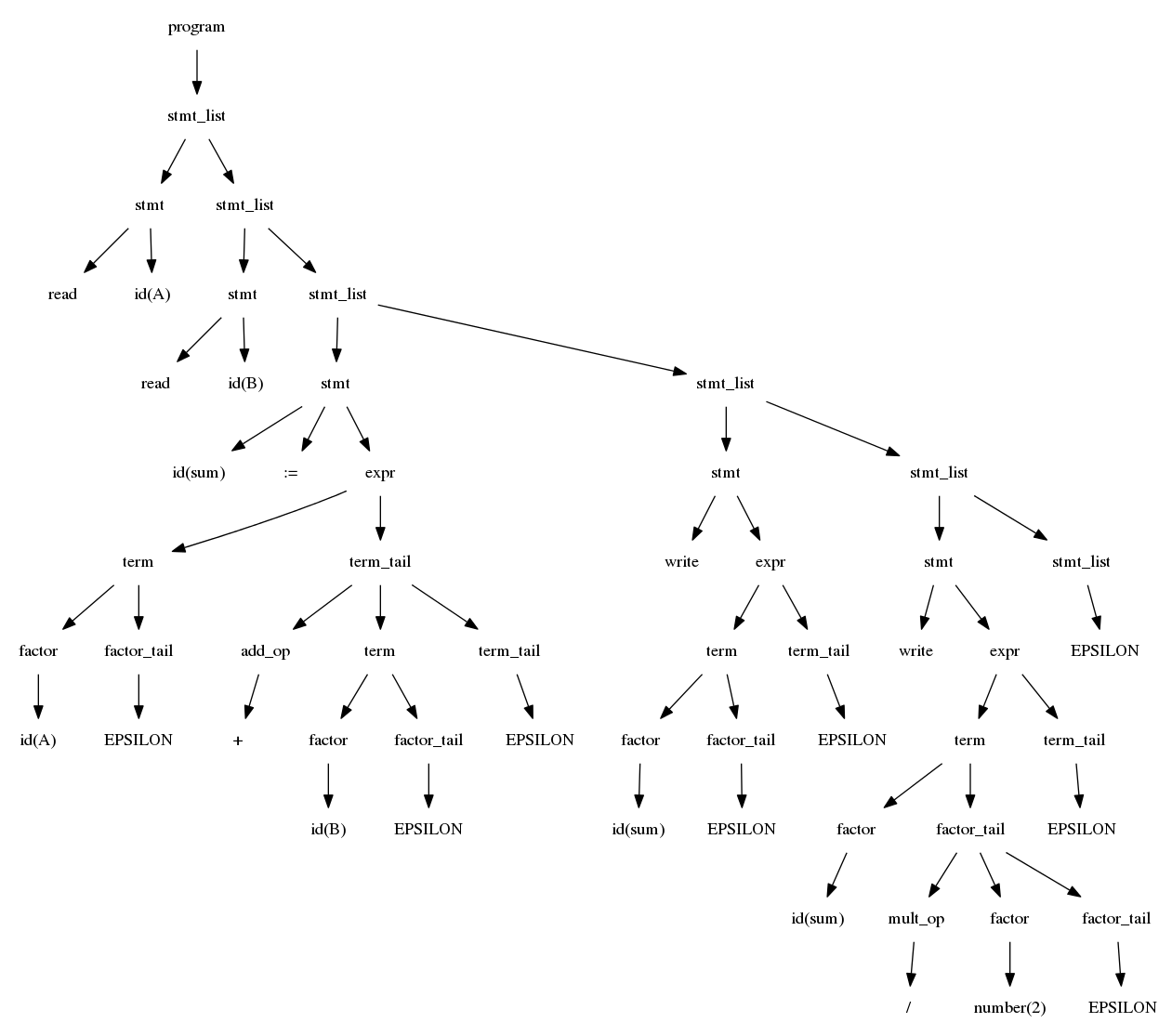
While figure 2.21 shows that for small examples like the grammar for example 2.24, it is easy to see the first and follow sets, it quickly grows more challenging as grammars grow bigger.
Your text on pp.79-82 gives definitions and algorithms for computing predict, first, and follow sets.
$$stmt \rightarrow if\ condition\ thenclause\ elseclause\ | otherstmt$$ $$thenclause \rightarrow then\ stmt$$ $$elseclause \rightarrow then\ stmt\ |\ \epsilon$$
Shift and reduce are the fundamental actions in bottom-up parsing
Page 87: "...a top-down parser's stack contains a list of what the expects to see in the future; a bottom-up parser's stack contains a record of what the parser has already seen in the past."
Stack contents Remaining input
-------------------------------- ---------------
(nil) A, B, C;
id(A) , B, C;
id(A), B, C;
id(A), id(B) , C;
id(A), id(B), C;
id(A), id(B), id(C) ;
id(A), id(B), id(C);
id(A), id(B), id(C) id_list_tail
id(A), id(B) id_list_tail
id(A), id_list_tail
id_list$$idlist \Rightarrow id\ idlisttail \Rightarrow id,\ id\ idlisttail$$ $$\Rightarrow id,\ id,\ id\ idlisttail \Rightarrow id, id, id;$$