It does not generate an interrupt.
| Real Time Systems: Notes |
A cyclic executive can be coded very simply, without the complexity of implementing preemption.
The discussion of clock-driven scheduling in Chapter 5 of Liu tends to hide this important fact by mixing in various forms of preemptive scheduling.
Here, we will look a non-preemptive cyclic executives, starting with a series of solutions to an example problem.
The following example is intended to illustrate a set of simple but interesting timing constraints, and how one might design a cyclic executive to satisfy these timing constraints. The example is made up, but has some characteristics that are found in actual real-time systems.
In general, aperiodic tasks do not fit well into the cyclic scheduling model. The solutions shown here stretch the limits of what one can do with a nonpreemptive cyclic executive. Strictly speaking, this problem cannot be solved using a pure cyclic schedule. The implementation developed here is not completely deterministic, since (as will be seen) the pattern of execution depends on the aperiodic arrivals of event E. However, we can verify logically that the timing requirements will always be satisfied.
The example evolved from a simpler one, in which the task A1 had a simple periodic constraint. Conversion to a maximum separation constraint made the example more interesting, but also more complicated and more subtle. In retrospect, it might be pedagogically better to start with the original simpler problem, with a pure periodic timing requirement for A1. One could then introduce the separation constraint model as a variation, to show how one would handle more general kinds of timing constraint. It would also help if the description also made a clearer separation of the treatment of the aperiodic (separation constraint) of task A2 from the periodic task A1.
The example attempts to follow a sound software engineering method, starting with a set of given requirements and constraints, deriving further design constraints, developing trial solutions, rejecting solutions that do not satisfy the requirements, and verifying that the final solution satisfies all of the requirements.
The following requirements are imposed on the software by the system design and the real world:
Let us assume these requirements have some tolerance for error, say ±10%.
In a real software development environment, the algorithms and code for the actions A1 and A2 would probably be developed by different specialists than are responsible for design of the code that schedules the execution. The person who is assigned to write the executive must take the timing requirements above and attempt to satisfy them. If this cannot be done, the only recourse would be to go back to the specialists who imposed these requirements and ask whether they can find a way to relax them.
The following constraints are imposed by the real world:

The first two are contraints on the implementation, imposed by budget and the choice of hardware. If a solution cannot be found, these might be relaxed by spending some more on hardware. For example, constraint (4) might be relaxed by developing hardware that generates an interrupt when event E occurs, and constraint (5) might be relaxed by providing a hardware timer that can generate an interrupt might be provided. However the additional hardware would cost more money. In some real-time systems even a small increase in hardware cost could make a large difference in profitability for the end product. The example proceeds on the assumption that these constraints cannot be relaxed.
The third constraint (6) is on the real-world event E. We need some such constraint, or we will not be able to tell how often to poll for E. In practice, if this information is not originally given the software engineer would need to go back to the system engineers to get them to agree on some such constraint.
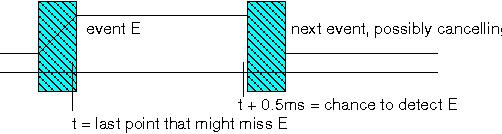
The shaded zone in the diagram indicates an interval during which polling might return an ambiguous value. If we sample the input during this interval we may not detect E, and so would need to sample again before the next transition. There is a similar ambiguous interval at the next transition. To detect the state change that constitutes event E, we need
The following worst-case execution time are consequences of hardware speed, algorithm choice, and coding.
The following additional constraint is imposed to make scheduling feasible, based on knowledge of the real world.
We hope this is true, but if not, we interpret this as permission to simply ignore events that are closer than 50ms. In some systems this might actually be a requirement, to ignore events that are closer than 50ms. For example, this might be based on the assumption that they are due to bouncing of an electrical contact.
The following are consequences, which affect scheduling.
In (12) we analyze A2, which is an aperiodic task, as if it were a periodic task. This is a case of over-allocation, which is typical of trying to force aperiodic tasks into a periodic scheduling framework. We will not need to execute A2 every 5ms, since the minimum inter-arrival time of event E is 50ms. However, event E could happen at any time, so to achieve the desired 5ms reponse time with a static cyclic schedule, we need to reserve 2ms out of every 5ms for executing A2. Thus, although the worst-case long-term CPU utilization of A2 is only 2/50 = 4%, the ``local'' competition A2 gives to other tasks is equivalent to that of a task with 2/5 = 40% CPU utilization.
The following are consequences of using a non-preemptive executive.
The reason for dividing A1 is to allow the polling for E to take place. We do not have to divide A2, since we only execute A2 after E has been detected, and we don't need to poll again for E until 50ms later. This gives time to complete A2.
The following is close to a solution to the requirements above. This executive has a defect. The defect will be pointed out and corrected further below. However, it may be instructive to try to spot it before reading the explanation.
loop
-- executive processing (poll for E, and check time)
if E then
Stage_of_A2:=1;
end if;
if Clock>=Time_for_A1 then
if Stage_of_A1/=0 then recover_from_missed_deadline; end if;
Stage_of_A1:=1;
Time_for_A1:=Time_for_A1+0.01;
end if;
-- main processing
if Stage_of_A2/=0 then
--give A2 priority, due to shorter deadline
Do_A2;
Stage_of_A2:=0;
elsif Stage_of_A1/=0 then
Do_A1(Stage_of_A1);
Stage_of_A1:=Stage_of_A1+1;
if Stage_of_A1 = End_of_A1 then Stage_of_A1:= 0; end if;
end if;
end loop;
Here, the variables Stage_of_Ai are used to indicate the stage of completion of each of the two actions. Stage_of_Ai = 0 means action Ai has completed, and Stage_of_Ai /= 0 means action Ai is supposed to be executing. Stage_of_A1 goes through values 1, 2, and 3, reflecting the 3 subactions of A1.
The following is an example of a possible execution trace. P denotes execution of the code to poll for E and check the Clock. 1 denotes execution of A1, and 2 denotes execution of A2. The granularity is not intended to be precise.
E Clock=Time_for_A1 | | v v PPPP22222222222222222222PPPPPPP1111P1111P11PPPPPPPPPPPPPP
Let's check whether the requirements are satisfied.
A1 is scheduled every 10ms. Only the higher priority task A2 can prevent it from executing, and this delays A1 at most 2.1ms.
The earliest completion time of A1 is no earlier than 1ms after its release time:
Clock=Time_for_A1
| A1 has completed
V V
PPP1111P1111P11PPPPPPPPPPPPPPP...
---0---------1---------2---------3---------4-----ms
The worst-case response time for A1 is when E occurs at a time A1 is due to execute.
E, and Clock=Time_for_A1
| A1 has completed
V V
PPP22222222222222222222P1111P1111P11PPPPPPPPPPPPPP...
---0---------1---------2---------3---------4---------ms
The absolute jitter for A1 is the execution time of A2, plus the overhead of one extra iteration of the polling code, i.e. about 2.1ms.
Here, we discover a defect. The jitter of 2.1ms means the interval between two executions of A1 might be as large as 12.1 ms, which exceeds the maximum separation constraint (requirement (1)) of 10ms ± 10%.
There are several ways we might try to fix this:
Let us explore these each in more detail.
To change priorities, so that A2 cannot preempt A1, we reorder the branches of the if-statement:
if Stage_of_A1/=0 then
Do_A1(Stage_of_A1);
Stage_of_A1:=Stage_of_A1+1;
if Stage_of_A1 = End_of_A1 then
Stage_of_A1:= 0;
end if;
elsif Stage_of_A2/=0 then -- give A2 lower priority
Do_A2;
Stage_of_A2:=0;
end if;
Since scheduling is not preemptive, we still have a problem if A2 is already running when the time to execute A1 comes.
Time_For_A1 E detected | A1 completes at time ~ 1.03 |Time_For_A1 A1 | | || done V V VV V PPP111111PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP2222222222211111PPPP ---0----1----2----3----4----5----6----7----8----9----0----1----2----3-ms
We could combat this by dividing A2 into subactions, as we did A1, but that would not be enough, since right now, A1's period gives no slack time. This leaves us with the other two approaches.
To shorten the period of A1, to allow for preemption by A2, we change the code as follows:
Time_for_A1:=Time_for_A1+0.008;
This gives us a period of 0.008, leaving 2ms for A1 to be blocked by A2, and still complete within 10ms of its last execution.
Since we have no other tasks, we can also drop the explicit period of A1 entirely, so that it executes whenever there is idle time:
Stage_of_A1 := 1;
loop
-- main processing
if E then --give A2 priority, due to shorter deadline
Do_A2;
else
Do_A1(Stage_of_A1);
Stage_of_A1:=Stage_of_A1+1;
if Stage_of_A1 = End_of_A1 then Stage_of_A1:= 1; end if;
end if;
end loop;
We will now execute A1 approximately every millisecond, except when we need to execute A2.
The worst case response time for A2 occurs when A1 is executing.
Clock=Time_for_A1
|E occurs
|| E is detected
|| | A2 completes
VV V V
PPP111122222222222PPPPPP...
---0---------1---------2--------3--------4--------ms
The division of A1 into 0.4ms stages ensures that E is detected within 0.5ms, and A2 will start no later than that time. It will then complete no later than 0.5+2=2.5ms after E occurs.
We have divided the subactions of A1 small enough that the interval between checks for E does not exceed 0.5ms. As argued above, we do not need to divide A2, since E should not reoccur within 50ms of the last occurrence.
Questions:
What if we want to ensure we do not poll for E any closer than 0.5ms? This might be required, for example, to debounce a contact. You should be able to modify the code above to do that?
Time is divided into equal-sized ``frames''.
Length of frame = "minor cycle" Length of schedule = "major cycle" = k * minor_cycle
Each job must be scheduled to execute entirely within one frame.
Item 3 above requires heavy-duty preeptive executive, that can suspend threads, and later resume them. (That is the sort of executive assumed by much of the discussion in Chapter 5 of Liu.)
The cyclic executive paradigm is usually used for tasks with periodic timing constraints, though it can be adapted to other kinds of timing constraints.
| task | period | execution time |
|---|---|---|
| A | 10 | 4 |
| B | 20 | 6 |
| C | 60 | 5 |
Below is a possible cyclic schedule for these tasks, using a frame size of 10.
AAAA AAAA AAAA AAAA AAAA AAAA
BBBBBB BBBBBB BBBBBB
CCCCCC
0----5----10---15---20---25---30---35---40---45---50---55---60

The schedule shown above could be implemented in several ways. One way is via a table.
More general executives might require more complicated tables, but
the cyclic schedule above could be represented very simply, by the
string
"AB0AC0AB0A0AB0A0".
Here "0" indicates the end of the work to be done in a time interval of 10 milliseconds. An executive could be implemented using this table.
procedure Executive is
Schedule: constant String:= "AB0AC0AB0A0AB0A0";
T: Time:= Clock;
I: Schedule'Range:= Schedule'First;
begin
loop
T:= T+ 0.01;
while Clock < T loop null; end; loop;
-- idle until time to start next 10ms "frame" of schedule
loop
I:= I+1;
if I = Schedule'Length then I:= Schedule'First; end if;
case Schedule (I) is
when "A" => A;
when "B" => B;
when "C" => C;
when others => exit;
end case;
end loop;
end loop;
end Executive;
If the tasks have timing constraints other than simple periodic constraints, it is still possible to adapt a cyclic scheduling approach, as in the example we are trying to solve. In this example, we have no pure periodic timing constraints. Instead we have a cyclic task with a maximum separation constraint and an aperiodic task with a response time constraint.
Reconsider the A1/A2/E example, but now suppose there is a timer that can be set to interrupt once every 0.0005 second.
Suppose we first try using 8ms as the major period, since that worked for our other example.
major period = 8ms minor period = 4ms
Frame 0 Frame 1 V V 222222222222111111 222222222222 0-----1-----2-----3-----4-----5-----6-----7-----(repeat) ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
V = frame boundary
^ = clock interrupt point,
where polling for
E and updating of a periodic clock
T will be done
2 = indicates time reserved for
A2
1 = time reserved for
A1
We have reserved time for A2 in both frames, since we are concerned about the response time requirement of 5ms, even though we know we will never have to use this time in two consecutive frames.
T: Integer:= 0;
T_Tick: constant:= 0.0005; -- 0.5ms
Clock_Modulus: constant:= 32; -- period of counter T (below)
Major_Period: constant:= 16; -- 16 clock ticks = 8ms
Minor_Period: constant:= 8; -- 8 clock ticks = 4ms
Frame: Integer:=0;
A1_Done, A2_Done : Boolean:= True;
procedure Handler is
begin
if E then
if not A2_done then recover_from_A2_overrun; end if;
A2_done:= false;
end if;
-- we could also check for missed deadlines here
if T <= Clock_Modulus then T:=T+1; else T:=0; end if;
end Handler;
procedure Executive is
begin
Install_Timer_Handler(Handler'Access);
loop
while Is_Before(T,Frame) loop null; end loop;
-- Frame-T < -Clock_Modulus/2 or 0 < Frame-T < Clock_Modulus/2
Frame:= Frame+Minor_Period;
if Frame>=Clock_Modulus then Frame:=Frame-Clock_Modulus;
if not A2_done then
A2; A2_done:= true;
end if; -- takes ~ 2 ms
if Frame mod Major_Cycle = 0 then A1; end if; -- takes ~ 1 ms
end loop;
end Executive;
Note also that sometimes the work ``scheduled'' in a frame does not actually need to be done. In particular, we are scheduling a chance to execute A2 in every frame, but we only actually execute it if we have detected E in the last frame interrupt.
The correctness of Frame mod Major_Cycle = 0 depends on Clock_Modulus (32) being divisible by Major_Cycle (16).
The ability to implement the function Is_Before depends on Clock_Modulus being greater than two times the maximum separation of times being compared, i.e. 2 ⋅ 8 = 16.
(More about modular time will be explained below.)
The maximum separation for executions of A1 is 8ms + 2ms = 10ms.
Frame 0 Frame 1 Frame 2
V V V
1111 22222222 222222221111
0---1---2---3---4---5---6---7---8---9---0---1--- ms
^ ^
execution of A1 done next exec
of A1 done
Question: What is the worst-case response time, from the time an event E happens to the time action A2 is completed?
Answer: ~ 4ms (for next frame) + 2ms (for A2 to complete) = 6ms
Frame 0 Frame 1 Frame 2
V V V
222222222222
0-----1-----2-----3-----4-----5-----6-----7-----8-----9 ms
^* ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
| E is detected A2 starts A2 completes
E occurs
This is not good enough. We need a response time of 5ms.
To improve the response time, we can try changing frame size. (Remember that it must be an exact multiple of the clock tick.) Suppose we try 3ms. The canonical schedule is:
V V 222222222222111111222222222222 0-----1-----2-----3-----4-----5-----(repeat) ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
The worst-case response time for E is now about 3ms + 2ms = 5ms.
V V V V 111111 222222222222 0-----1-----2-----3-----4-----5-----6--... ^* ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | E is detected A2 starts A2 completes E occurs
Task A1 is now executing every 6ms. That is OK, since we have only a maximum separation constraint for A1, but it would not be very good if we have any other work to do, since we are wasting CPU capacity, executing A1 more often than necessary.
We could try a different frame size, to see if we could separate the executions of A1 further, to reduce the CPU load. For example, with a frame size of 2ms we could use a major period of 8ms:
V V V V 222222222222.....................................................50ms 111111 0-----1-----2-----3-----4-----5-----6-----7-----(repeat) ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
The worst-case response time for E is now ~2ms+2ms = 4ms:
V V V V
222222222222
0-----1-----2-----3-----4-----5-----6-----7-----(repeat)
^* ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
E detected A2 starts A2 completes
The maximum separation of executions of A1 is now ~8ms+2ms = 10ms:
V V V V V 111111 222222222222111111 0-----1-----2-----3-----4-----5-----6-----7-----8-----9-----0-----1----- ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
V V V V V V 111111 222222222222 222222222222222222222222 0-----1-----2-----3-----4-----5-----6-----7-----8-----9-----0-----1----- ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
This reduces the number of executions of A1, but requires us to reserve more CPU capacity for A2 to meet its 5ms response time constraint.
To implement this, we would have to force A2 not to execute on even frames, by changing the code of the loop, perhaps as follows:
if not A2_done and then Frame mod 2 = 0 then
------------------------
A2; -- takes ~ 2 ms
A2_done:= true;
elsif Frame mod Major_Cycle = 0 then
A1; -- takes ~ 1 ms
end if;
Back in the beginning, we estimated the local processor utilization of A2 to be 40%. This was the effective local utilization during the interval that A2 will be competing with other jobs. We used this for the purpose of estimating whether A2 could be scheduled in the interval between when E occurs and 5ms later. It allowed us to be sure we could complete A2 on time, regardless of when it arrives.
If we just look at the cyclic schedule above, with 2ms minor cycle and 8ms major cycle, we see that A2 is reserved 2ms out of every 4ms, so the effective utilization is 50%. This number is higher because fitting the schedule into frames forced us to cut the effective deadline for A2 from 5ms down to 4ms.
Now, if we are interested in the big picture, as to how much time might be left for other (lower priority) work, the answer is different. The global CPU utilization of A2 is at most 2ms/50ms, or 4%, since E cannot occur more than once in 50 ms. Adding in 1% for polling for A1, we have a total CPU utilization of only 15%.
How much could we increase the total utilization (by increasing the execution times of A1 and A2) and still be able to meet deadlines using this cyclic executive (with frame size of 2ms)?
In other words, how much room do we have for increasing the execution times of A1 and A2, without overloading the system?
We can't increase the execution time of A2 without risking a separation of more than 10ms between executions of A1.
0 2 4 6 8 0 2 4 6 8 0 |---|---|---|---|---|---|---|---|---|---| 11 222211e1 = 1
If we try increasing the execution time of A1, we find we can do that quite a bit without causing A1 to miss a deadline.
0 2 4 6 8 |---|---|---|---|---|---|---|---|---| 2222111111111111e1 = 6
However, we now have a problem with A2, e.g.
0 2 4 6 8 10
|---|---|---|---|---|---|---|---|---|
1111111111111111111
^E detected
When E is detected we can't execute A2 since A1 is still executing.
What we want in this case is the following.
0 2 4 6 8 10
|---|---|---|---|---|---|---|---|---|
11111111222211111111
^E detected, so we execute A2
e1 = 6Since we would only need to break A1 up into 4 subactions, this may be feasible. If it needed to broken up much finer, we should start considering preemptive scheduling.
| Period | Exec. Time |
|---|---|
| p0 = 1 | e0 = 0.2 |
| p1 = 2 | e1 = 0.3 |
| p2 = 2 | e2 = 0.4 |
| p3 = 4 | e3 = 0.8 |
hyperperiod = 4 = LCM of task periods
major Cycle = hyperperiod, or larger multiple
minor Cycle = 1 or smaller, subject to other constraints
0 1 2 3 4
[---------[---------[---------[---------[ (Gantt chart)
001111 002222 001111 002222
33333333
The following is not an acceptable schedule for implementation by cyclic executive.
0 1 2 3 4 [---------[---------[---------[---------[ (Gantt chart) 00111133333333002222001111 002222
Task 3 does not fit within one minor cycle, so the minor-cycle interrupt does not provide any "fire wall" to protect tasks 0 and 2 from overflows of task 3.
If task 3 overflows, we do not detect it until time 2, by which time task 0 and task 2 may have already missed their deadlines.
To fit task 3 in, we must divide it, say into tasks 3a and 3b:
| Period | Exec. Time |
|---|---|
| p3a = 4 | e3a = 0.4 |
| p3b = 4 | e3b = 0.4 |
0 1 2 3 4 [---------[---------[---------[---------[ (Gantt chart) 001111aaaa002222 001111bbbb002222
p3 = 4/3, e3 = 0.3
minor cycle = 0.5, does not divide 4/3
major cycle = 4
0 1 2 3 4
[----[----[----[----[----[----[----[----[ (Gantt chart)
333 333 333
[ [ [ [
approx. approx.
deadline deadline
of T3 of T3
In general, the minor cycle need not divide the task periods,
but the minor cycle and the periods must all divide the major cycle.
where ei = compute time of task
i
and m = minor cycle(a.k.a. frame size)
The above material is from Baker & Shaw, ``The Cyclic Executive Model and Ada'', The Journal of Real-Time Systems 1, 7-25 (1989).
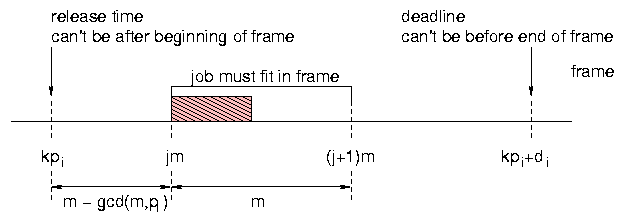
Between every release time and the corresponding deadline there must be a complete frame. The closest these two events can be without being coincident is when they are separated by gcd(m, pi).
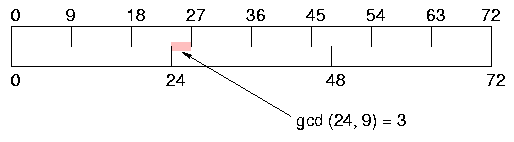
On at least one modern commercial jetliner the avionics computer uses a periodic scheduling approach to divide the use of the CPU between the software of various subsystems, which are produced independently by different manufacturers. The executive divides the processor time into slices, of different sizes. Each subsystem is viewed by the executive as a different "task", that executes periodically. Internally, the subsystems do their own finer-grained scheduling.
For example, if there are two subsystems, we might choose to divide up the time between them, 2/3 for subsystem Ai and 1/3 for subsystem
B:
|----|----|----|----|----|----| ... AAAAABBBBBBBBBBAAAAABBBBBBBBBB
We could do this with a timer-driven cyclic executive. We would have to take care how we choose the minor and major periods, since it limits the response time of each subsystem. For example, the worst-case asynchronous event response time of a task in the example above is going to be three minor periods. On the other hand, we don't want to choose the minor period too short, or we will spend too much CPU time in interrupt-handling overhead.
For maximum flexibility, the executive should be preemptive, so that we can fit jobs/subsystems that have large execution into the schedule without delaying other jobs.
For moderate-sized systems, some of these problems can be handled by using tools, such as timing analyzers and schedule-builders, to automatically generate (and regenerate) the schedule.
Contrast point 3 to the situation in the real-time clock example, where a two-part clock may be updated by an interrupt handler while a background process is reading it.
Hardware timers, like wall clocks, keep track of modular time; that is, the clock periodically wraps around.
Let t stand for any point in (unbounded) real time, and C(t) stand for the value of clock C at time t. If C is a modular clock with modulus P, then for all real numbers t
,where δ is the quantum (tick size) of the clock C.
For a ``perfect'' clock with tick size P and ideal discrete time, C(t) = t - ⌊t/P⌋ ⋅P
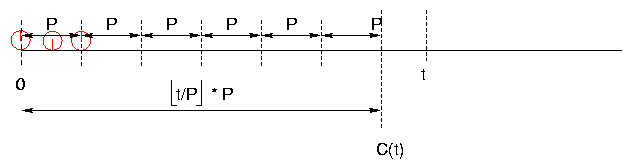
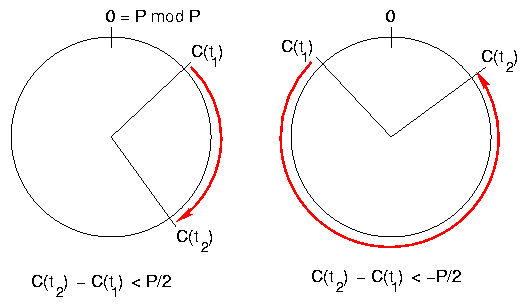
If we know that two real times t1 and t2 are not more than P/2 apart, we can infer the relative ordering of t2 in linear time by looking at the (modular) clock values C(t1) and C(t2). The relationship t1 < t2 holds iff one of the following two cases applies:
When one is working with cyclic executives, one naturally tends to use modular arithmetic on integers. This is potentially erroneous, as we shall see.
When scheduling a periodic task with period D starting at time S, if we had a non-modular clock (that never overflowed) we would schedule the task to execute at times S+kD, for k = 0,1,2,3,... .
This does not necessarily work for a periodic clock unless P is an exact integer multiple of D. For example, it does not work is when S = 0, D = 3, and P = 4. That is shown in the second figure below.
linear
+----+----+----+----+----+----+----+----+----+----+----+ clock
0 1 2 3 4 5 6 7 8 9 10 11
+----+----+----+----+----+----+----+----+----+----+----+ clock mod 3
0 1 2 0 1 2 0 1 2 0 1 2
^ ^ ^ ^
If the clock never wraps around, we can use mod directly to determine the deadlines and release times of a periodic task.
mod 4
+----+----+----+----+----+----+----+----+----+----+----+ clock
0 1 2 3 0 1 2 3 0 1 2 3
+----+----+----+----+----+----+----+----+----+----+----+ clock mod 3
0 1 2 0 0 1 2 0 0 1 2 0
^ ^ ^ ^
If the clock is modular, beware of situations where the task period does not divide the clock modulus exactly. Here, the clock period is 4 and ^ marks the release times of a task with period 3.
We cannot safely use (clock mod 3) = 0 as our test for when to execute a task with period three in the example above, and in general we cannot safely use a similar expression for any other period that does not exactly divide the fundamental moduls of our real time clock.
This applies when we have a clock that counts mod 2**16, or 2**32, but we may not notice the problem in testing, sind the clock wrap-around occurs rather infrequently.
To avoid this, we must take care that the periods of tasks are all exact divisors of the clock period, or that the clock never wraps.
This is a timing anomaly similar to the ``year 2000'' problem; a programmer might not believe that the clock will ever wrap, but then if the system runs long enough, the clocks wraps.
File this one away with the floating-point time pitfall.
Can you explain what is the problem in each case?
| © 1998, 2003, 2006 T. P. Baker. ($Id: staticscheduling.html,v 1.2 2008/08/25 11:18:48 baker Exp baker $) |